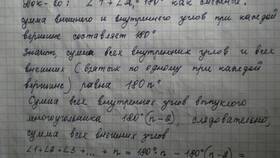Сумма внешних углов многоугольника - важная геометрическая характеристика, которая имеет постоянное значение для любых выпуклых многоугольников. Рассмотрим методы ее вычисления.
Содержание
Сумма внешних углов многоугольника - важная геометрическая характеристика, которая имеет постоянное значение для любых выпуклых многоугольников. Рассмотрим методы ее вычисления.
Основное свойство суммы внешних углов
| Тип многоугольника | Сумма внешних углов |
| Выпуклый n-угольник | 360° |
| Невыпуклый многоугольник | Также 360° при правильном подсчете |
Доказательство теоремы о сумме внешних углов
- В каждой вершине многоугольника внешний и внутренний углы в сумме дают 180°
- Сумма внутренних углов n-угольника равна (n-2)×180°
- Общая сумма всех пар (внутренний + внешний угол) равна n×180°
- Вычитаем сумму внутренних углов: n×180° - (n-2)×180° = 360°
Практическое вычисление
Для правильного n-угольника:
Каждый внешний угол = 360° / n
Сумма всех внешних углов = n × (360° / n) = 360°
Пример для пятиугольника:
- Количество сторон (n) = 5
- Величина каждого внешнего угла = 360° / 5 = 72°
- Сумма внешних углов = 5 × 72° = 360°
Особые случаи
| Фигура | Внешние углы |
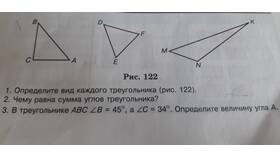
| Треугольник | 3 по 120° (сумма 360°) |
| Квадрат | 4 по 90° (сумма 360°) |
| Правильный шестиугольник | 6 по 60° (сумма 360°) |
Пошаговая инструкция для произвольного многоугольника
- Определить количество вершин (n) многоугольника
- Измерить каждый внутренний угол (α₁, α₂, ..., αₙ)
- Вычислить каждый внешний угол как 180° - αᵢ
- Сложить все внешние углы
- Убедиться, что сумма равна 360°
Важные замечания:
- Теорема верна для простых (несамопересекающихся) многоугольников
- Внешний угол может быть отрицательным (для вогнутых углов)
- При обходе против часовой стрелки положительные углы считаются положительными
- Для звездчатых многоугольников сумма также равна 360°
Знание этого свойства позволяет решать различные геометрические задачи, связанные с многоугольниками, и проверять корректность их построения.
